Zadanie nr 8976573
W trójkącie 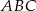 poprowadzono środkową
poprowadzono środkową 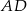 . Kąt
. Kąt 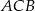 ma miarę
ma miarę 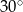 , a kąt
, a kąt 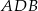 ma miarę
ma miarę 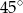 . Jaka jest miara kąta
. Jaka jest miara kąta 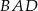 ?
?
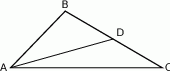
A) 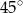 B)
B) 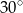 C)
C) 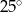 D)
D) 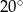 E)
E) 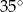
Rozwiązanie
Dorysujmy wysokość 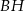 i połączmy punkt
i połączmy punkt 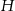 z punktem
z punktem 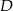 .
.
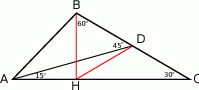
Popatrzmy na trójkąt prostokątny 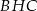 . Odcinek
. Odcinek 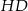 jest w nim środkową, więc
jest w nim środkową, więc 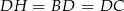 (bo każdy z tych odcinków jest równy promieniowi okręgu opisanego na trójkącie
(bo każdy z tych odcinków jest równy promieniowi okręgu opisanego na trójkącie 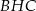 ; okrąg ten ma środek w punkcie
; okrąg ten ma środek w punkcie 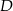 ). To jednak oznacza, że trójkąt
). To jednak oznacza, że trójkąt 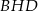 jest równoboczny (bo jest równoramienny i ma kąt
jest równoboczny (bo jest równoramienny i ma kąt 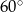 ). Zatem
). Zatem 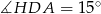 . Z drugiej strony
. Z drugiej strony
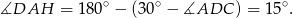
To oznacza, że trójkąt 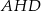 jest równoramienny, czyli
jest równoramienny, czyli 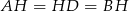 , co z kolei oznacza, że trójkąt
, co z kolei oznacza, że trójkąt 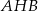 jest równoramienny i prostokątny. Zatem
jest równoramienny i prostokątny. Zatem 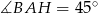 , czyli
, czyli 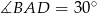 .
.
Odpowiedź: B

