/Konkursy/Zadania testowe/Geometria/Planimetria

Zadanie nr 6416017

Dodaj do ulubionych
Dodaj do rozwiązanych

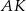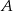Dwusieczna AK kąta A w trójkącie 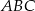ABC podzieliła ten trójkąt na dwa trójkąty o równych polach. Wówczas trójkąt 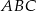ABC jest na pewno
A) równoboczny B) równoramienny C) prostokątny D) ostrokątny E) rozwartokątny

Rozwiązanie

Zróbmy rysunek.

PIC

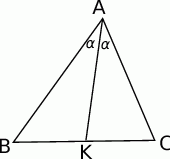
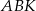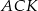Ponieważ trójkąty ABK i ACK mają wspólną wysokość, to z równości ich pól wynika, że 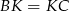BK = KC . Z drugiej strony, z twierdzenia o dwusiecznej

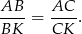
AB-- AC-- BK = CK .

Skąd dostajemy 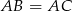AB = AC .

Inny sposób wykazania tej równości może opierać się na wzorze z sinusem na pole trójkąta

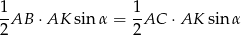
1 1 -AB ⋅AK sin α = -AC ⋅AK sinα 2 2

 
Odpowiedź: B

Wersja PDF