Zadanie nr 1013271
Za 4 jednakowe swetry i spodnie zapłacono 384 zł, a za sam sweter i spodnie 132 zł. Ile kosztuje sweter, a ile spodnie?
Rozwiązanie
Sposób I
Z podanych informacji wynika, że za 3 swetry zapłacono
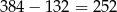
złote. Zatem sweter kosztuje
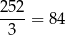
złote, a spodnie 132-84=48 zł.
Sposób II
Możemy też ułożyć układ równań. Niech  będzie ceną swetra, a
będzie ceną swetra, a 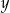 ceną spodni.
ceną spodni.
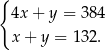
Odejmujemy od pierwszego równania drugie
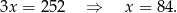
Stąd 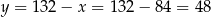 .
.
Odpowiedź: Sweter: 84 zł, spodnie: 48 zł.

