Zadanie nr 1031376
Zbieramy z Olkiem znaczki i wczoraj Olek mi powiedział, że ma już 155 znaczków angielskich, francuskich i hiszpańskich. Francuskich ma 2 razy więcej niż hiszpańskich, a angielskich o 39 mniej niż francuskich i hiszpańskich razem. To jednak niemożliwe, uzasadnij dlaczego Olek musiał się pomylić.
Rozwiązanie
Sposób I
Oznaczmy przez  liczbę znaczków hiszpańskich. Wtedy znaczków francuskich jest
liczbę znaczków hiszpańskich. Wtedy znaczków francuskich jest 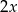 , a angielskich
, a angielskich
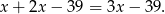
Wiemy ponadto, że
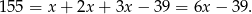
Stąd
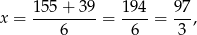
co oczywiście nie jest możliwe, bo 97 nie dzieli się przez 3.
Sposób II
Oznaczmy ilości odpowiednich znaczków przez 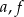 i
i 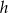 . Wiemy zatem, że
. Wiemy zatem, że
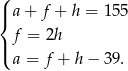
Podstawiając za  w pierwszym równaniu z trzeciego mamy
w pierwszym równaniu z trzeciego mamy
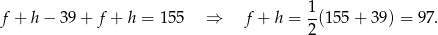
Uwzględniając, że 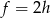 , mamy
, mamy
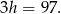
Ale 97 nie dzieli się przez 3, zatem podane informacje muszą być błędne.

