Zadanie nr 1145767
Na rysunku przedstawiono okrąg o środku 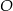 , który jest styczny do wszystkich boków trapezu równoramiennego
, który jest styczny do wszystkich boków trapezu równoramiennego 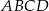 . Ramiona
. Ramiona 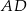 i
i 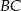 są styczne do tego okręgu odpowiednio w punktach
są styczne do tego okręgu odpowiednio w punktach 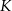 i
i 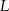 . Kąt wypukły
. Kąt wypukły 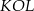 ma miarę
ma miarę 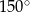 .
.
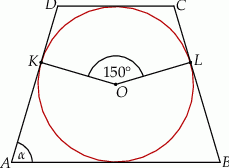
Miara  kąta ostrego tego trapezu jest równa
kąta ostrego tego trapezu jest równa
A) 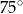 B)
B) 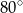 C)
C) 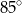 D)
D) 
Rozwiązanie
Sposób I
Niech 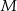 będzie punktem styczności danego okręgu i podstawy
będzie punktem styczności danego okręgu i podstawy 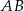 .
.
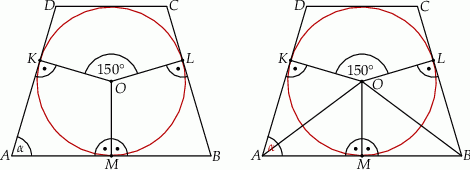
Trapez jest równoramienny, więc
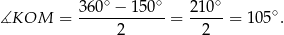
W czworokącie 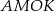 mamy
mamy
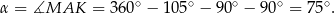
Sposób II
Tak jak poprzednio, niech 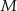 będzie punktem styczności danego okręgu i podstawy
będzie punktem styczności danego okręgu i podstawy 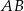 . Cztery trójkąty prostokątne
. Cztery trójkąty prostokątne 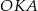 ,
, 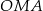 ,
, 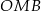 i
i 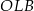 są przystające oraz
są przystające oraz
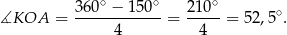
Stąd
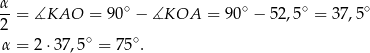
Sposób III
Niech 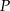 będzie punktem wspólnym ramion
będzie punktem wspólnym ramion 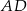 i
i 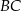 .
.
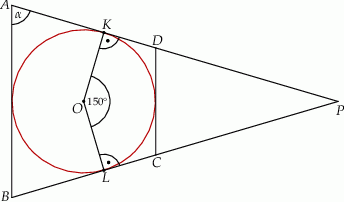
Ponieważ promienie 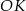 i
i 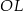 są prostopadłe do ramion trapezu, w czworokącie
są prostopadłe do ramion trapezu, w czworokącie 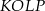 mamy
mamy
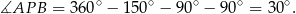
Trójkąt 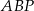 jest równoramienny, więc
jest równoramienny, więc
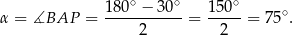
Odpowiedź: A

