/Szkoła podstawowa

Zadanie nr 1288301

Dodaj do ulubionych
Dodaj do rozwiązanych

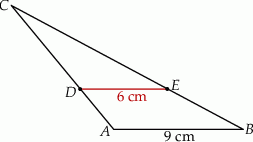
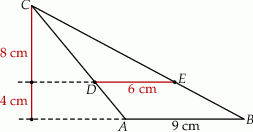
Na rysunku przedstawiono trójkąt 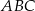ABC , w którym 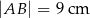|AB | = 9 cm oraz odcinek 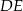DE równoległy do boku 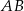AB trójkąta, którego długość jest równa 6 cm.

PIC

Pole trójkąta 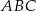ABC jest równe 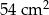54 cm 2 , a pole trapezu 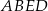ABED jest o 25% większe od pola trójkąta 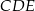CDE . Oblicz wysokość trapezu ABED .

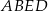Rozwiązanie

Sposób I

Jeżeli oznaczymy przez 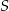S pole trójkąta 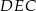DEC , to wiemy, że pole trapezu 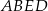ABED jest równe

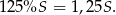
125%S = 1,25S.

W takim razie

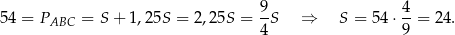
9 4 54 = PABC = S + 1 ,25S = 2,2 5S = --S ⇒ S = 54 ⋅--= 2 4. 4 9

To oznacza, że pole trapezu jest równe

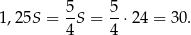
1,25S = 5S = 5-⋅24 = 3 0. 4 4

Jeżeli teraz oznaczymy przez 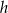h wysokość trapezu, to

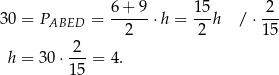
6 + 9 1 5 2 30 = PABED = ------⋅h = ---h / ⋅ --- 2 2 15 h = 30 ⋅-2-= 4. 15

Sposób II

Tym razem skorzystamy z podobieństwa trójkątów 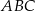ABC i DEC .

PIC

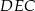Wysokość 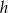h trójkąta 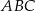ABC możemy obliczyć z podanego pola

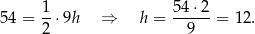
1 54 ⋅2 5 4 = --⋅9h ⇒ h = ------= 12. 2 9

Zatem wysokość trójkąta 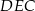DEC (podobnego do 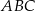ABC w skali 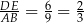DE- = 6 = 2 AB 9 3 ) jest równa

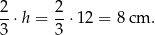
2 2 --⋅h = --⋅12 = 8 cm . 3 3

To z kolei oznacza, że wysokość trapezu 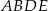ABDE jest równa

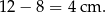
12− 8 = 4 cm .

 
Odpowiedź: 4 cm

Wersja PDF