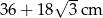Zadanie nr 1763649

W trójkącie równobocznym wysokość jest o 3 cm krótsza od boku trójkąta. Oblicz pole i obwód tego trójkąta.

Rozwiązanie

Możemy zacząć od szkicowego rysunku.

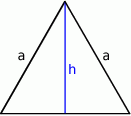
Skorzystamy ze wzorów na wysokość i pole trójkąta równobocznego:

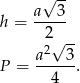
√ -- h = a--3- 2 a 2√ 3- P = ------. 4

Z treści zadania i ze wzoru na wysokość mamy równanie

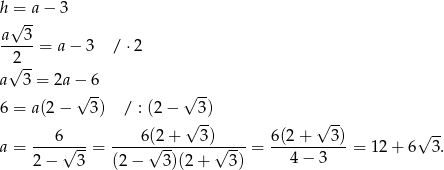
h = a − 3 √ -- a--3- 2 = a− 3 / ⋅2 √ -- a 3 = 2a −√ 6- √ -- 6 = a(2 − 3) / : (2− 3) √ -- √ -- ---6---- ----6(2-+---3)----- 6(2+----3)- √ -- a = √ --= √ -- √ -- = 4 − 3 = 12 + 6 3. 2 − 3 (2− 3)(2 + 3)

Obwód tego trójkąta jest więc równy

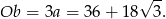
√ -- Ob = 3a = 36 + 18 3.

Pole trójkąta możemy policzyć na dwa sposoby:

Sposób I

Korzystamy z podanego wcześniej wzoru

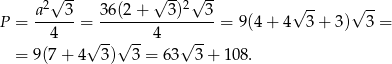
-- -- -- a2√ 3 36(2 + √ 3)2√ 3 √ -- √ -- P = ------= ----------------= 9(4 + 4 3 + 3) 3 = 4 √ --√ -- 4 √ -- = 9(7+ 4 3) 3 = 63 3+ 108.

Sposób II

Możemy też skorzystać ze wzoru:

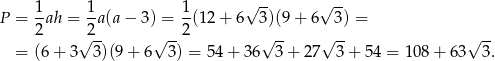
√ -- √ -- P = 1ah = 1-a(a− 3 ) = 1(1 2+ 6 3)(9+ 6 3) = 2 √2-- √ --2 √ -- √ -- √ -- = (6+ 3 3)(9 + 6 3) = 5 4+ 36 3+ 27 3 + 54 = 108+ 63 3.

Odpowiedź: Pole: 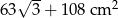√ -- 63 3 + 108 cm 2 , obwód: 36 + 18 √ 3 cm