/Szkoła podstawowa

Zadanie nr 3189971

Dodaj do ulubionych
Dodaj do rozwiązanych

Basia jest o 8 lat młodsza od Kasi. Za 30 lat będą miały razem 116 lat. Ile lat ma każda z nich obecnie?

Rozwiązanie

Sposób I

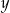Jeżeli oznaczymy przez x i y wiek odpowiednio Basi i Kasi, to mamy układ równań

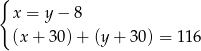
{ x = y − 8 (x + 30) + (y + 30) = 1 16

Odejmujemy od pierwszego równania drugie (żeby skrócić x ).

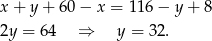
x + y+ 60− x = 116 − y + 8 2y = 64 ⇒ y = 32.

Zatem 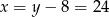x = y − 8 = 24 .

Sposób II

Skoro za 30 lat będą miały łącznie 116 lat, to teraz mają łącznie 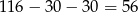116 − 3 0− 3 0 = 56 lat. Jeżeli oznaczymy przez x wiek Basi, to mamy równanie

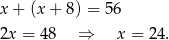
x + (x + 8 ) = 56 2x = 48 ⇒ x = 24.

Kasia ma więc 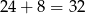24 + 8 = 3 2 lata.  
Odpowiedź: Basia ma 24 lata, a Kasia 32 lata.

Wersja PDF