/Szkoła podstawowa

Zadanie nr 4157150

Dodaj do ulubionych
Dodaj do rozwiązanych

W zalanej kopalni zainstalowano 3 pompy wypompowujące wodę z zalanych sztolni. Pierwsza pompa pracująca sama wypompowałaby wodę w ciągu 12 dni, druga w ciągu 15 dni, a trzecia 20 dni. Pierwsze trzy dni pierwsza i trzecia pompa pracowały wspólnie. Następnie włączono dodatkowo drugą pompę. Jak długo trwało wypompowywanie wody z kopalni?

Rozwiązanie

Sposób I

Wiemy, że pierwsza pompa w ciągu jednego dnia wypompowuje 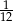1- 12 całej wody, druga 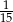1 15 , a trzecia 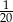1 20- . Jeżeli oznaczymy liczbę dni pracy pomp przez n to mamy równanie

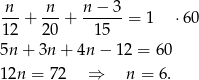
n-+ -n-+ n−--3-= 1 ⋅60 12 20 15 5n + 3n+ 4n − 12 = 60 12n = 72 ⇒ n = 6.

Sposób II

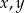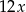Jeżeli oznaczmy dzienne wydajności pomp przez x,y i z to wiemy, że w kopalni jest 1 2x wody (bo pierwsza pompa wypompowuje ją w 12 dni). Ponadto

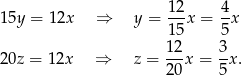
1 2 4 1 5y = 12x ⇒ y = ---x = -x 1 5 5 2 0z = 12x ⇒ z = 12-x = 3-x. 20 5

Jeżeli teraz przez n oznaczymy liczbę dni, w trakcie których wszystkie trzy pompy pracowały razem to mamy równanie

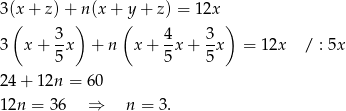
3(x + z)+ n (x+ y+ z) = 12x ( ) ( ) 3 x+ 3x + n x+ 4x + 3-x = 12x / : 5x 5 5 5 24 + 1 2n = 60 12n = 36 ⇒ n = 3.

Zatem wodę wypompowano w 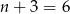n + 3 = 6 dni.  
Odpowiedź: 6 dni

Wersja PDF