Zadanie nr 4238535

Maciek pływa w basenie o długości 25 m. W jednym końcu basenu głębokość wynosi 3 m, a w drugim 1,5 m. Kąt nachylenia dna basenu do powierzchni wody jest stały.

Czy Maciek ’ma grunt’ pod stopami w odległości 10 m od płytszego końca basenu? Przyjmij, że wzrost Maćka wynosi 180 cm, a basen jest całkowicie wypełniony wodą.
Oblicz pojemność basenu, w którym pływa Maciek. Szerokość basenu wynosi 10 m.

Rozwiązanie

Zacznijmy od rysunku.

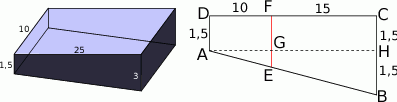
Obliczymy długość odcinka 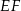. Na mocy twierdzenia Talesa mamy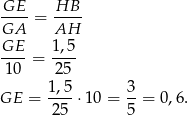
$GE HB ----= ---- GA AH GE--= 1,5- 1 0 25 1,5- 3- GE = 25 ⋅1 0 = 5 = 0,6.$

Zatem

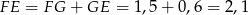
$F E = FG + GE = 1,5 + 0,6 = 2 ,1$

Czyli Maciek nie będzie miał gruntu pod nogami.
Odpowiedź: Nie, nie będzie miał gruntu.
Aby obliczyć objętość myślimy o basenie jak o graniastosłupie, który w podstawie ma boczną ścianę basenu. Pole trapezu w podstawie jest równe:
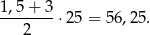
$1 ,5 + 3 --------⋅2 5 = 56,25. 2$

Objętość jest więc równa

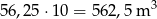
$3 56,25 ⋅10 = 56 2,5 m$

Odpowiedź: