Zadanie nr 4406029
Z kwadratowego kawałka materiału o boku 1,6 m wykonano obrus. Na brzegi obrusa naszyto ozdobną taśmę. Taką samą taśmę naszyto również na powierzchnię obrusa, tworząc wzór w następujący sposób.
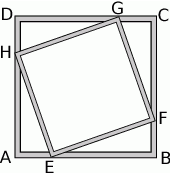
- Każdy bok obrusa podzielono dwoma punktami na odcinki, których długości mają się do siebie jak 1:2:1.
- Ozdobną taśmą łączono co drugi z wyznaczonych punktów. Powstały dwa czworokąty.
Oblicz, ile taśmy zużyto na ozdobienie obrusa, jeżeli dodatkowo na szwy przeznaczono 15 cm tej taśmy. Wynik podaj z dokładnością do 0,1 m.
Rozwiązanie
Wykonajmy najpierw schematyczny rysunek opisanej sytuacji.
Na brzegi obrusa zużyto
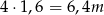
taśmy.
Aby obliczyć ile taśmy potrzeba na mniejszy kwadrat, obliczymy boki trójkąta prostokątnego 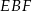 .
.
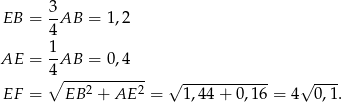
W sumie potrzeba więc (są dwa małe kwadraty!)
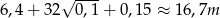
Odpowiedź: 16,7m

