Zadanie nr 4412795
Trzy pracujące jednocześnie pompy wypompowały 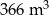 wody, przy czym wydajność pierwszej pompy była o 20% niższa niż wydajność trzeciej pompy, a wydajność drugiej pompy była o 20% niższa niż wydajność pierwszej pompy. Łączny koszt pracy pomp wyniósł 1464 zł, przy czym koszt pracy każdej z pomp był proporcjonalny do jej wydajności. Jaki był koszt pracy każdej z pomp?
wody, przy czym wydajność pierwszej pompy była o 20% niższa niż wydajność trzeciej pompy, a wydajność drugiej pompy była o 20% niższa niż wydajność pierwszej pompy. Łączny koszt pracy pomp wyniósł 1464 zł, przy czym koszt pracy każdej z pomp był proporcjonalny do jej wydajności. Jaki był koszt pracy każdej z pomp?
Rozwiązanie
Jeżeli oznaczymy przez  ilość wody wypompowanej przez trzecią pompę, to pierwsza pompa wypompowała
ilość wody wypompowanej przez trzecią pompę, to pierwsza pompa wypompowała 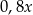 , a druga
, a druga
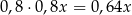
wody. Mamy więc równanie
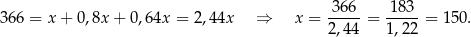
W takim razie kolejne pompy wypompowały odpowiednio
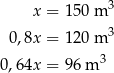
wody. To oznacza, że koszt pracy pomp był odpowiednio równy
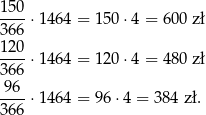
Odpowiedź: 600 zł, 480 zł i 384 zł

