/Szkoła podstawowa

Zadanie nr 4745759

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż układ równań 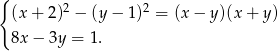{ 2 2 (x+ 2) − (y − 1 ) = (x− y)(x + y) 8x− 3y = 1.

Rozwiązanie

Korzystamy ze wzorów skróconego mnożenia:

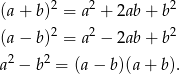
2 2 2 (a+ b) = a + 2ab+ b (a− b)2 = a2 − 2ab+ b2 2 2 a − b = (a− b)(a+ b).

Przekształcamy pierwsze równanie układu.

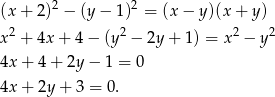
2 2 (x + 2) − (y − 1) = (x − y )(x + y) x2 + 4x + 4 − (y2 − 2y + 1) = x2 − y2 4x + 4 + 2y − 1 = 0 4x + 2y + 3 = 0.

Mamy więc układ

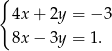
{ 4x + 2y = − 3 8x − 3y = 1.

Sposób I

Odejmujemy od drugiego równania pierwsze pomnożone przez 2 (żeby skrócić x ).

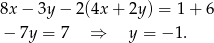
8x − 3y− 2(4x + 2y) = 1+ 6 − 7y = 7 ⇒ y = − 1.

Z pierwszego równania mamy więc

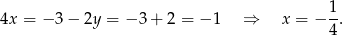
1 4x = − 3 − 2y = − 3 + 2 = − 1 ⇒ x = − 4-.

Sposób II

Podstawiamy 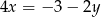4x = − 3− 2y z pierwszego równania do drugiego.

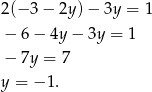
2(− 3− 2y)− 3y = 1 − 6 − 4y − 3y = 1 − 7y = 7 y = − 1.

Stąd

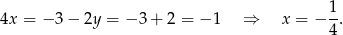
1- 4x = − 3 − 2y = − 3 + 2 = − 1 ⇒ x = − 4 .

 
Odpowiedź: 1 x = − 4, y = − 1

Wersja PDF