/Szkoła podstawowa

Zadanie nr 5151538

Dodaj do ulubionych
Dodaj do rozwiązanych

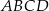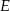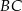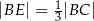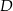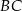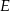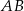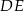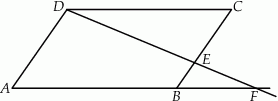
W równoległoboku ABCD punkt E jest takim punktem boku BC , że |BE | = 13|BC | . Z wierzchołka D poprowadzono prostą przecinającą bok BC w punkcie E . Proste AB i DE przecinają się w punkcie 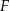F (zobacz rysunek). Wykaż, że pole trójkąta 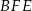BF E stanowi 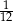-1 12 pola równoległoboku ABCD .

PIC

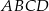Rozwiązanie

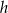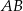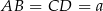Oznaczmy przez h wysokość równoległoboku opuszczoną na bok AB oraz niech AB = CD = a .

PIC

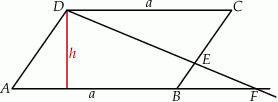
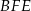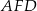Zauważmy, że trójkąty BF E oraz AF D są podobne (bo mają równe kąty) oraz znamy skalę 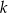k ich podobieństwa

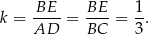
k = -BE- = BE--= 1-. AD BC 3

W szczególności 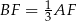BF = 13 AF , czyli 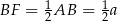BF = 12AB = 12a oraz

PBFE = 1PAFD = 1-⋅ 1-⋅AF ⋅h = -1-⋅ 3a ⋅h = -1-ah = 1-PABCD . 9 9 2 1 8 2 1 2 12
Wersja PDF