/Szkoła podstawowa

Zadanie nr 5265322

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest trójkąt prostokątny. Wykaż, że suma pól kół o średnicach będących przyprostokątnymi trójkąta jest równa polu koła o średnicy równej przeciwprostokątnej.

Rozwiązanie

Zaczynamy od rysunku

PIC

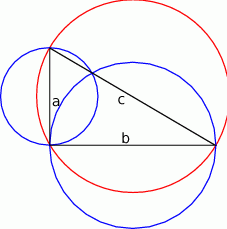
Najpierw obliczmy pole koła o średnicy c

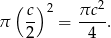
( ) 2 π c- 2 = πc--. 2 4

Odcinki 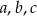a,b,c są bokami trójkąta prostokątnego, więc

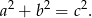
a2 + b2 = c2.

Teraz policzmy sumę pozostałych pól

( ) ( ) 2 2 2 π a- 2 + π b- = πa--+ πb-- = 2 2 4 4 2 2 2 = π(a--+-b-)-= πc--. 4 4
Wersja PDF