/Szkoła podstawowa

Zadanie nr 5639661

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest liczba dwucyfrowa. Jeśli dopiszemy na końcu tej liczby 5, to otrzymamy liczbę o 482 większą od danej. Jeśli zaś dopiszemy na końcu tej liczby dwucyfrowej 10, to otrzymamy liczbę o 5257 większa od danej. Wyznacz tę liczbę dwucyfrową.

Rozwiązanie

Sposób I

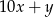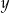Jeżeli 10x + y jest szukaną liczbą dwucyfrową (x – cyfra dziesiątek, y – cyfra jedności), to mamy układ równań

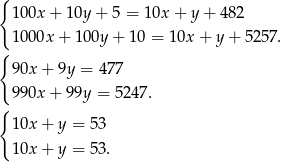
{ 10 0x+ 10y + 5 = 1 0x+ y+ 482 10 00x + 100y + 1 0 = 10x + y + 525 7. { 90x + 9y = 477 99 0x+ 99y = 5 247. { 10x + y = 53 10x + y = 53.

Zatem szukana liczba to 53. Przy okazji widać, że jeden z warunków jest niepotrzebny.

Sposób II

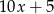Jeżeli oznaczymy szukaną liczbę przez x , to po dopisaniu z prawej strony cyfry 5 otrzymujemy liczbę 10x + 5 . Mamy więc równanie

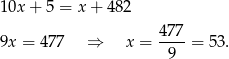
10x + 5 = x + 482 477 9x = 477 ⇒ x = ----= 53. 9

Druga z podanych informacji jest zbędna.  
Odpowiedź: 53

Wersja PDF