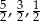Zadanie nr 5788829
Dane są dwa okręgi zewnętrznie styczne oraz styczne wewnętrznie do trzeciego. Środki okręgów tworzą trójkąt równoramienny o bokach długości 1 i 2. Znajdź długości promieni tych okręgów (rozważ dwa przypadki).
Rozwiązanie
Zaczynamy od rysunku.
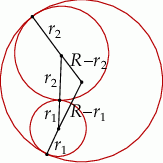
Jeżeli oznaczymy przez 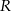 promień dużego okręgu, a przez
promień dużego okręgu, a przez 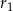 i
i 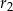 promienie mniejszych, to trójkąt, o którym mowa w zadaniu ma boki długości
promienie mniejszych, to trójkąt, o którym mowa w zadaniu ma boki długości 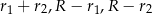 . Musimy teraz się zastanowić, które dwa z nich są równe. Jeżeli
. Musimy teraz się zastanowić, które dwa z nich są równe. Jeżeli 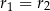 , to musi być
, to musi być
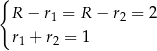
(bo trójkąt musi mieć boki 2,2,1, nie ma trójkąta o bokach 1,1,2). Z drugiej równości mamy 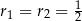 , co nam daje
, co nam daje 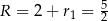 .
.
Jeżeli natomiast 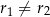 , to
, to 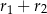 musi być równe
musi być równe 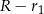 lub
lub 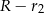 . Ewentualnie zmieniając oznaczenia, możemy założyć, że zachodzi pierwszy z tych przypadków, czyli
. Ewentualnie zmieniając oznaczenia, możemy założyć, że zachodzi pierwszy z tych przypadków, czyli
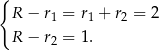
Mamy zatem
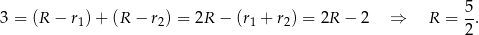
Stąd 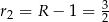 i
i 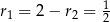 .
.
Odpowiedź: 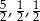 lub
lub