/Szkoła podstawowa

Zadanie nr 6353389

Dodaj do ulubionych
Dodaj do rozwiązanych

W składzie pewnego pociągu ekspresowego wagony pierwszej klasy stanowią 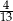143 łącznej liczby wagonów pierwszej i drugiej klasy. W tym samym pociągu jest o 10 wagonów drugiej klasy więcej, niż jest wagonów pierwszej klasy. Ile łącznie wagonów pierwszej i drugiej klasy jest w tym pociągu?

Rozwiązanie

Sposób I

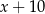Jeżeli wagonów pierwszej klasy jest x , to wagonów drugiej klasy jest x+ 10 . Wiemy ponadto, że wagony pierwszej klasy stanowią 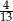413- wszystkich wagonów, więc

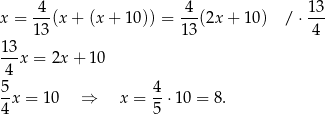
x = -4-(x+ (x+ 10)) = -4-(2x + 10) / ⋅ 13 13 1 3 4 13 --x = 2x + 10 4 5x = 10 ⇒ x = 4⋅ 10 = 8. 4 5

Łączenie jest więc

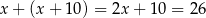
x+ (x+ 10) = 2x + 1 0 = 26

wagonów.

Sposób II

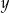Jeżeli oznaczymy przez x i y liczby wagonów pierwszej i drugiej klasy, to informacje podane w treści zadania prowadzą do układu równań

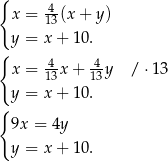
{ x = 413(x+ y) { y = x + 1 0. x = 4-x+ 4-y / ⋅1 3 13 13 y = x + 1 0. { 9x = 4y y = x + 1 0.

Podstawiamy teraz 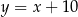y = x + 10 z drugiego równania do pierwszego.

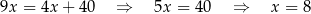
9x = 4x + 40 ⇒ 5x = 40 ⇒ x = 8

Łączenie jest więc

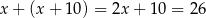
x+ (x+ 10) = 2x + 1 0 = 26

wagonów.  
Odpowiedź: 26

Wersja PDF