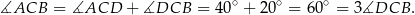/Szkoła podstawowa

Zadanie nr 6784998

Dodaj do ulubionych
Dodaj do rozwiązanych

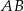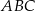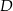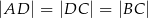Na boku AB trójkąta ABC znajduje się taki punkt D , że |AD | = |DC | = |BC | . Miara kąta 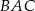BAC jest równa 40 ∘ .

PIC

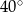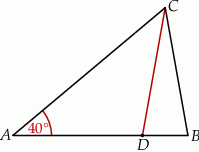
Uzasadnij, że miara kąta 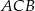ACB jest trzy większa od miary kąta BCD .

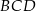Rozwiązanie

Wiemy, że trójkąt 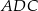ADC jest równoramienny, więc

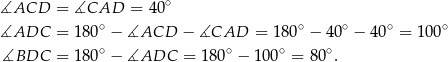
∡ACD = ∡CAD = 4 0∘ ∡ADC = 18 0∘ − ∡ACD − ∡CAD = 180∘ − 40∘ − 40∘ = 1 00∘ ∡BDC = 18 0∘ − ∡ADC = 180∘ − 100∘ = 80∘.

Trójkąt DBC też jest równoramienny, więc

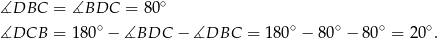
∘ ∡DBC = ∡BDC = 80 ∡DCB = 180∘ − ∡BDC − ∡DBC = 1 80∘ − 80∘ − 80∘ = 20 ∘.

Zatem rzeczywiście

∡ACB = ∡ACD + ∡DCB = 40∘ + 20∘ = 60∘ = 3∡DCB .
Wersja PDF