/Szkoła podstawowa

Zadanie nr 7044881

Dodaj do ulubionych
Dodaj do rozwiązanych

Na wycieczkę do kina miała pójść grupa 28 uczniów klasy IIb. Ostatecznie jednak liczba osób biorących udział w wycieczce zmniejszyła się o jedną osobę. Stało się tak, gdyż z wycieczki zrezygnowało 25% dziewcząt, oraz do grupy dołączyło kilku chłopców z klasy IIa i liczba chłopców biorących udział w wycieczce zwiększyła się o 25%. Ilu chłopców i ile dziewcząt wzięło udział w wycieczce?

Rozwiązanie

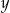Jeżeli oznaczymy przez x i y odpowiednio liczbę chłopców i dziewcząt, którzy początkowo mieli wziąć udział w wycieczce, to podane informacje prowadzą do układu równań

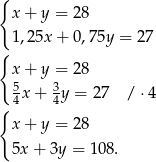
{ x + y = 2 8 { 1,25x + 0 ,7 5y = 27 x + y = 2 8 5 3 4x + 4y = 27 /⋅ 4 { x + y = 2 8 5x + 3y = 108.

Odejmujemy teraz od drugiego równania pierwsze pomnożone przez 3 i mamy

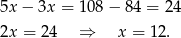
5x− 3x = 1 08− 84 = 24 2x = 24 ⇒ x = 12.

Stąd 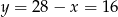y = 28 − x = 16 . To jednak nie koniec, bo musimy obliczyć ile osób faktycznie wzięło udział w wycieczce.

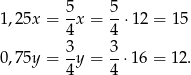
5- 5- 1,25x = 4x = 4 ⋅12 = 15 3 3 0,75y = -y = --⋅16 = 12 . 4 4

 
Odpowiedź: W wycieczce wzięło dział 15 chłopców i 12 dziewcząt.

Wersja PDF