/Szkoła podstawowa

Zadanie nr 7089549

Dodaj do ulubionych
Dodaj do rozwiązanych

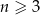Jeżeli n ≥ 3 , to liczbę przekątnych wielokąta wypukłego o n bokach można obliczyć ze wzoru

n-(n−--3). 2

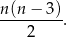
Wielokąt, który ma cztery razy więcej przekątnych niż boków ma A/B boków.
A) 10 B) 11
Liczba przekątnych wielokąta o 222 bokach jest liczbą C/D.
C) nieparzystą D) parzystą

Rozwiązanie

Musimy rozwiązać równanie

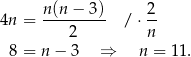
n(n − 3) 2 4n = --------- / ⋅-- 2 n 8 = n − 3 ⇒ n = 11 .

Liczba przekątnych 222–kąta jest równa

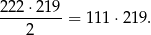
222⋅-219-= 1 11⋅ 219. 2

Oczywiście jest to liczba nieparzysta.  
Odpowiedź: B, C

Wersja PDF