/Szkoła podstawowa

Zadanie nr 7572602

Dodaj do ulubionych
Dodaj do rozwiązanych

W pierwszej urnie znajduje się 5 kul białych i 17 kul czarnych. W drugiej urnie znajduje się 16 kul białych i 34 kule czarne. Ile kul białych należy przełożyć z drugiej urny do pierwszej, aby wylosowanie kuli białej z obu urn było jednakowo prawdopodobne?

Rozwiązanie

Sposób I

Jeżeli prawdopodobieństwa wybrania białej kuli w obu urnach mają być takie same, to stosunek liczby kul białych do czarnych musi być taki sam w obu urnach. W drugiej urnie jest dwa razy więcej kul czarnych niż w pierwszej urnie, więc tak samo musi być z kulami białymi. Taka sytuacja będzie miała miejsce, gdy przełożymy dwie białe kule z drugiej urny do pierwszej – wtedy w pierwszej urnie będzie 7, a w drugiej 14 białych kul. Prawdopodobieństwa są wtedy odpowiednio równe

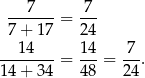
---7---= -7- 7 + 17 24 ---14--- 14- -7- 14 + 34 = 48 = 24 .

Sposób II

Jeżeli przełożymy n kul białych z drugiej urny do pierwszej, to opisana w treści zadania równość prawdopodobieństw sprowadza się do równania

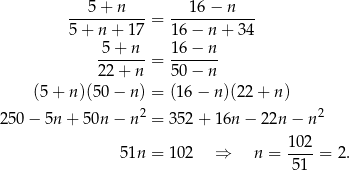
5 + n 16 − n ----------- = ------------ 5 + n + 17 1 6− n+ 34 -5-+-n- = 1-6−--n 2 2+ n 5 0− n (5 + n )(50− n) = (16 − n )(22+ n) 250 − 5n + 50n − n2 = 352 + 1 6n− 22n − n 2 102 5 1n = 102 ⇒ n = ----= 2 . 51

Musimy więc przełożyć dwie białe kule z drugiej urny do pierwszej.  
Odpowiedź: Należy przełożyć dwie kule białe.

Wersja PDF