Zadanie nr 7642997
Na boku 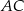 trójkąt równobocznego
trójkąt równobocznego 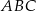 o polu równym
o polu równym 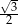 zbudowano równoramienny trójkąt prostokątny
zbudowano równoramienny trójkąt prostokątny 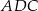 .
.
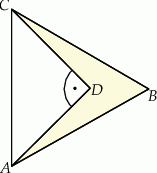
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole czworokąta 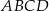 jest równe jest równe 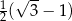 . . | P | F |
Obwód czworokąta 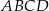 jest równy jest równy 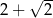 . . | P | F |
Rozwiązanie
Jeżeli oznaczymy przez  długość boku trójkąta równobocznego
długość boku trójkąta równobocznego 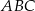 , to z podanego pola mamy
, to z podanego pola mamy
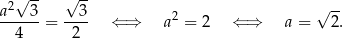
To oznacza, że przyprostokątne trójkąta 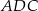 są równe
są równe 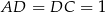 (bo trójkąt ten to połówka kwadratu o boku 1). W takim razie obwód czworokąta
(bo trójkąt ten to połówka kwadratu o boku 1). W takim razie obwód czworokąta 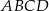 jest równy
jest równy
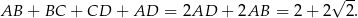
Jego pole jest równe
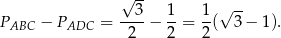
Odpowiedź: P, F

