Zadanie nr 7939212
W pewnym zakładzie pracy każdy z pracowników codziennie montuje taką samą liczbę jednakowych podzespołów. Pracownicy potrzebowali 12 dni roboczych, aby wykonać zamówienie. Gdyby wydajność każdego z pracowników była wyższa o 20%, to wykonaliby zamówienie w
A) 8 dni B) 9 dni C) 10 dni D) 11 dni
Rozwiązanie
Sposób I
Jeżeli wydajność pracownika rośnie o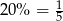 
, to w ciągu 5 dni pracownik wykona taką samą pracę jaką początkowo wykonałby w 6 dni. W takim razie całe zamówienie zostanie wykonane w 10 dni.
Sposób II
Jeżeli oznaczymy przez 
dzienną wydajność wszystkich pracowników to wiemy, że realizacja całego zamówienia wymaga nakładów pracy w ilości 
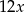. Po zwiększeniu wydajności do 
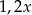liczba dni 
potrzebnych do realizacji zamówienia spełnia równanie
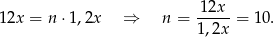
Odpowiedź: C
