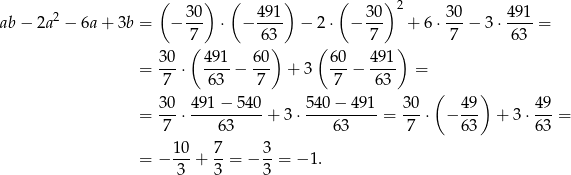Zadanie nr 8111407
Wykaż, że jeżeli 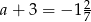 i
i 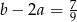 , to wartość wyrażenia
, to wartość wyrażenia 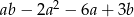 jest równa
jest równa 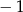 .
.
Rozwiązanie
Sposób I
Przekształcamy dane wyrażenie.
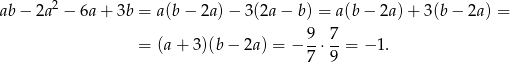
Sposób II
Wiemy, że
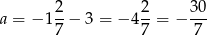
i
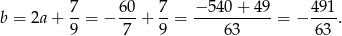
Stąd
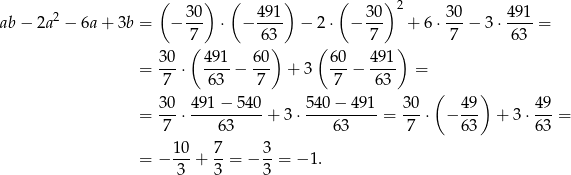
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli 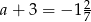 i
i 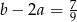 , to wartość wyrażenia
, to wartość wyrażenia 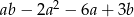 jest równa
jest równa 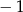 .
.
Sposób I
Przekształcamy dane wyrażenie.
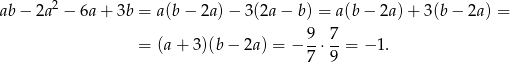
Sposób II
Wiemy, że
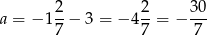
i
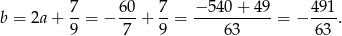
Stąd