Zadanie nr 8159905
Punkt kratowy to miejsce przecięcia się linii kwadratowej siatki. Pole wielokąta, którego wierzchołki znajdują się w punktach kratowych kwadratowej siatki na płaszczyźnie, można obliczyć ze wzoru Picka:
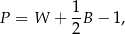
gdzie 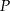 oznacza pole wielokąta,
oznacza pole wielokąta, 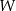 – liczbę punktów kratowych leżących wewnątrz wielokąta, a
– liczbę punktów kratowych leżących wewnątrz wielokąta, a 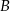 – liczbę punktów kratowych leżących na brzegu tego wielokąta.
– liczbę punktów kratowych leżących na brzegu tego wielokąta.
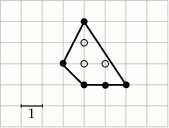
W wielokącie przedstawionym na rysunku 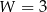 oraz
oraz 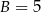 , zatem
, zatem 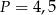 .
.
Wewnątrz pewnego wielokąta znajduje się 5 punktów kratowych, a na jego brzegu jest 6 punktów kratowych. Pole tego wielokąta jest równe
A) 6 B) 6,5 C) 7 D) 7,5
Rozwiązanie
Liczymy
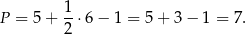
Odpowiedź: C

