Zadanie nr 8254154
Na wysokości 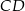 trójkąta równobocznego
trójkąta równobocznego 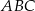 o boku długości 4 zbudowano kwadrat
o boku długości 4 zbudowano kwadrat 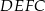 .
.
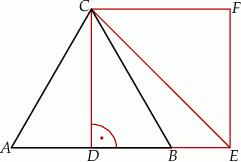
Pole trójkąta 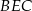 jest równe
jest równe
A) 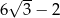 B)
B) 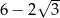 C)
C) 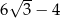 D)
D) 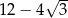
Rozwiązanie
Wysokość  trójkąta równobocznego
trójkąta równobocznego  jest równa
jest równa
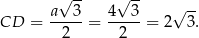
Sposób I
W takim razie
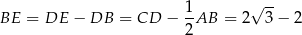
i pole trójkąta  jest równe
jest równe
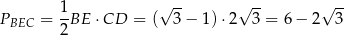
Sposób II
Pole interesującego nas trójkąta możemy obliczyć jako różnicę pól połówki kwadratu  i połówki trójkąta równobocznego
i połówki trójkąta równobocznego  . Mamy zatem
. Mamy zatem
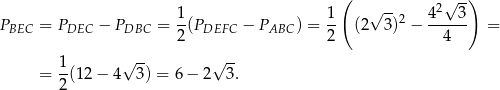
Odpowiedź: B

