Zadanie nr 8261405
Na rysunku przedstawiono prostokąt 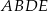 i trójkąt
i trójkąt 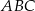 . Punkty
. Punkty 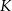 i
i 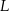 dzielą odcinki
dzielą odcinki 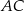 i
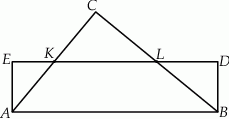
i 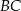 na połowy. Uzasadnij, że pole prostokąta
na połowy. Uzasadnij, że pole prostokąta 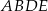 jest równe polu trójkąta
jest równe polu trójkąta  .
.
Rozwiązanie
Sposób I
Dorysujmy wysokość trójkąta  opuszczoną z wierzchołka
opuszczoną z wierzchołka  .
.
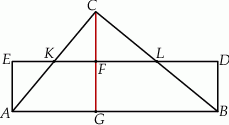
Zauważmy, że trójkąty 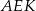 i
i 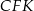 mają równe kąty oraz
mają równe kąty oraz 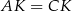 . W takim razie trójkąty te są przystające. Podobnie, trójkąty
. W takim razie trójkąty te są przystające. Podobnie, trójkąty 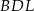 i
i 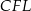 są przystające, więc
są przystające, więc
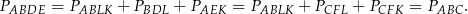
Sposób II
Tak jak poprzednio dorysowujemy wysokość trójkąta 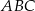 i zauważamy, że trójkąty
i zauważamy, że trójkąty 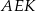 i
i 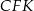 są przystające. W takim razie
są przystające. W takim razie