Zadanie nr 8384683
Paweł rzucił 5 razy zwykłą sześcienną kostką do gry. Zapisane kolejno wyniki rzutów utworzyły liczbę pięciocyfrową. Liczba ta jest parzysta i podzielna przez 9, a jej początkowe trzy cyfry to: 3, 1, 2. Ile oczek wyrzucił Paweł za czwartym i piątym razem? Podaj wszystkie możliwości.
Rozwiązanie
Szukamy liczby postaci 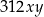 .
.
Sposób I
Liczba ta ma być podzielna przez 9, więc suma jej cyfr musi być podzielna przez 9. Ponieważ 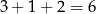 , suma cyfr otrzymanej liczby musi być równa 9 lub 18 (bo
, suma cyfr otrzymanej liczby musi być równa 9 lub 18 (bo  i
i 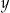 nie mogą być większe od 6). Jeżeli suma cyfr jest równa 18 to mamy
nie mogą być większe od 6). Jeżeli suma cyfr jest równa 18 to mamy 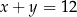 , czyli Paweł musiał wyrzucić 6 i 6.
, czyli Paweł musiał wyrzucić 6 i 6.
Jeżeli natomiast suma cyfr jest równa 9 to mamy 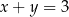 , czyli
, czyli 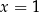 i
i 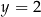 (bo
(bo 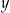 musi być parzyste).
musi być parzyste).
Są więc 2 liczby spełniające warunki zadania:
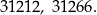
Sposób II
Skoro otrzymana liczba ma być liczbą parzystą, 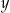 musi być parzyste, czyli
musi być parzyste, czyli 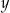 jest jedną z liczb: 2, 4, 6.
jest jedną z liczb: 2, 4, 6.
Jeżeli 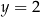 to mamy liczbę postaci
to mamy liczbę postaci 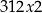 o sumie cyfr
o sumie cyfr 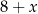 . Liczba ta jest podzielna przez 9 tylko dla
. Liczba ta jest podzielna przez 9 tylko dla 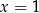 .
.
Jeżeli 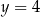 to mamy liczbę postaci
to mamy liczbę postaci 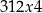 o sumie cyfr
o sumie cyfr 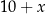 . Liczba ta nigdy nie będzie podzielna przez 9 (bo
. Liczba ta nigdy nie będzie podzielna przez 9 (bo 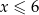 ).
).
Jeżeli 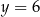 to mamy liczbę postaci
to mamy liczbę postaci 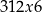 o sumie cyfr
o sumie cyfr 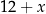 . Liczba ta jest podzielna przez 9 tylko dla
. Liczba ta jest podzielna przez 9 tylko dla 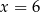 .
.
Są więc 2 liczby spełniające warunki zadania:
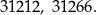
Odpowiedź: Paweł wyrzucił 1 i 2 lub 6 i 6.

