/Szkoła podstawowa

Zadanie nr 8618618

Dodaj do ulubionych
Dodaj do rozwiązanych

Element mechaniczny pewnego urządzenia ma kształt pełnego metalowego walca o wysokości 10 cm i promieniu podstawy 2 cm, który do połowy swojej wysokości jest umieszczony w gumowej półkuli o promieniu 6 cm. Oblicz stosunek objętości gumy do objętości metalu potrzebnych do wykonania tego elementu.

PIC

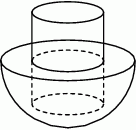
Rozwiązanie

Objętość walca o promieniu podstawy 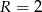R = 2 i wysokości 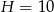H = 1 0 jest równa

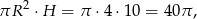
πR 2 ⋅H = π ⋅4⋅1 0 = 40π ,

a objętość połówki kuli o promieniu 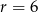r = 6 jest równa

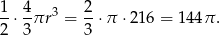
1-⋅ 4-πr3 = 2⋅ π ⋅216 = 1 44π . 2 3 3

Od tej objętości musimy jeszcze odjąć objętość wyciętej połówki walca, czyli objętość gumy jest równa

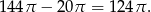
144π − 20π = 124π .

Interesujący nas stosunek objętości jest więc równy

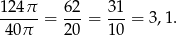
124π--= 62-= 31-= 3,1 . 40π 20 10

 
Odpowiedź: Stosunek objętości gumy do metalu jest równy 3,1.

Wersja PDF