Zadanie nr 8903028
Punkty 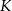 i
i 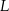 są środkami boków
są środkami boków 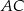 i
i 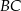 trójkąta
trójkąta 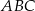 . Odcinki
. Odcinki 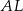 i
i 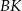 przecinają się w punkcie
przecinają się w punkcie 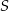 .
.
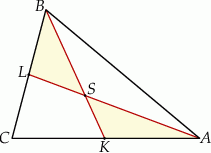
Uzasadnij, że pola trójkątów 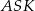 i
i 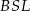 są równe.
są równe.
Rozwiązanie
Zauważmy, że odcinek 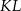 łączy środki boków trójkąta
łączy środki boków trójkąta 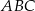 , więc jest równoległy do boku
, więc jest równoległy do boku 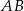 .
.
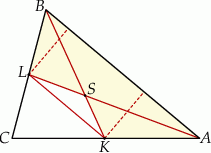
To oznacza, że trójkąty 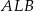 i
i 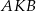 mają wspólną podstawę
mają wspólną podstawę 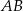 i równe wysokości opuszczone na tę podstawę. W takim razie mają równe pola
i równe wysokości opuszczone na tę podstawę. W takim razie mają równe pola