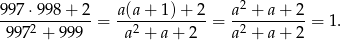Zadanie nr 8991133
Wykaż, że 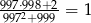 .
.
Rozwiązanie
Sposób I
Przekształcamy lewą stronę
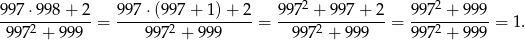
Sposób II
Przekształcamy lewą stronę
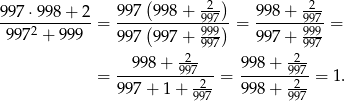
Sposób III
Tak jak poprzednio przekształcamy lewą stronę, ale podstawiamy 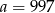 .
.
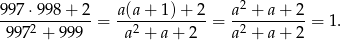
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że 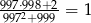 .
.
Sposób I
Przekształcamy lewą stronę
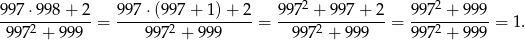
Sposób II
Przekształcamy lewą stronę
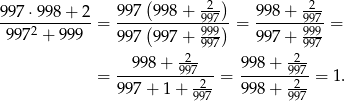
Sposób III
Tak jak poprzednio przekształcamy lewą stronę, ale podstawiamy 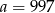 .
.