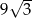/Szkoła podstawowa

Zadanie nr 9054386

Dodaj do ulubionych
Dodaj do rozwiązanych

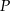Punkt P jest punktem przecięcia się wysokości trójkąta równobocznego. Jakie pole ma ten trójkąt, jeśli odcinek łączący punkt 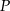P z wierzchołkiem trójkąta ma długość √ -- 2 3 ?

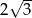Rozwiązanie

Zaczynamy od rysunku.

PIC

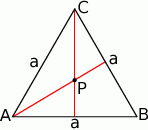
Będziemy korzystać ze wzoru na wysokość w trójkącie równobocznym o boku a

√ -- a--3- h = 2 ,

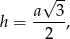
oraz z tego, że punkt 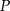P dzieli wysokość w stosunku 2:1 (licząc od wierzchołka).

Mamy równanie

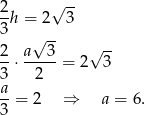
2 √ -- --h = 2 3 3 √ -- 2- a---3 √ -- 3 ⋅ 2 = 2 3 a- 3 = 2 ⇒ a = 6.

Zatem pole trójkąta jest równe

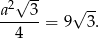
√ -- a2 3 √ -- --4---= 9 3.

 
Odpowiedź: √ -- 9 3

Wersja PDF