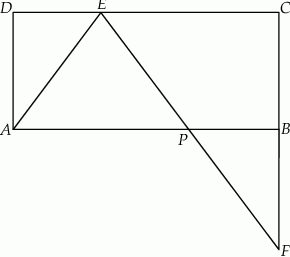
Zadanie nr 9082929
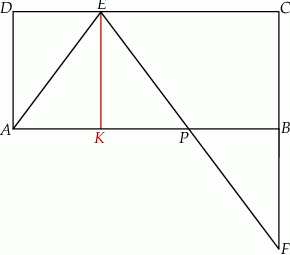
Dany jest prostokąt 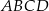 . Na boku
. Na boku 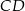 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 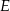 , że
, że 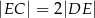 , a na przedłużeniu boku
, a na przedłużeniu boku 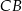 wybrano taki punkt
wybrano taki punkt 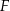 , że
, że 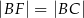 . Niech
. Niech 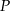 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 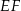 z prostą
z prostą 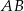 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 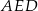 i
i 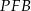 są przystające.
są przystające.
Rozwiązanie
Sposób I
Odcinek 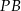 jest odcinkiem łączącym środki boków w trójkącie
jest odcinkiem łączącym środki boków w trójkącie 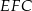 (bo
(bo 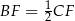 i
i 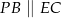 ), więc
), więc 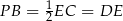 . Ponadto
. Ponadto
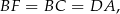
więc trójkąty prostokątne 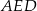 i
i 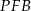 mają przyprostokątne tej samej długości. Trójkąty te są więc przystające.
mają przyprostokątne tej samej długości. Trójkąty te są więc przystające.
Sposób II
Niech 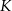 będzie rzutem punktu
będzie rzutem punktu 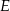 na bok
na bok 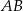 .
.
Trójkąty 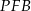 i
i 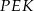 mają równe kąty (bo oba są prostokątne i
mają równe kąty (bo oba są prostokątne i 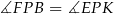 ) oraz
) oraz 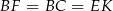 . To oznacza, że są przystające, czyli w szczególności
. To oznacza, że są przystające, czyli w szczególności
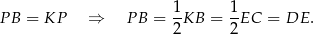
Wiemy ponadto, że 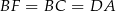 , więc przyprostokątne trójkątów prostokątnych
, więc przyprostokątne trójkątów prostokątnych 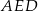 i
i 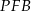 mają równe długości. Trójkąty te są więc przystające.
mają równe długości. Trójkąty te są więc przystające.

