Zadanie nr 9510096
Suma cyfr liczby trzycyfrowej podzielnej przez 5 jest równa 15. Jeśli zapiszemy cyfry tej liczby w odwrotnej kolejności, to otrzymamy liczbę o 198 większą od początkowej. Wyznacz liczbę początkową.
Rozwiązanie
Skoro szukana liczba dzieli się przez 5, to jej cyfrą jedności musi być 0 lub 5. Nie może to jednak być 0, bo wtedy liczba otrzymana przez zapisanie cyfr w odwrotnej kolejności będzie mniejsza od wyjściowej liczby. Zatem szukamy liczby postaci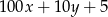 
. Z podanych informacji mamy układ równań
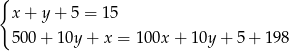
Przekształcamy drugie równanie
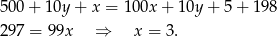
Z pierwszego równania układu mamy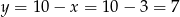 
. Zatem szukana liczba to 375.
Odpowiedź: 375
