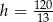/Szkoła podstawowa

Zadanie nr 9631728

Dodaj do ulubionych
Dodaj do rozwiązanych

Boki trójkąta prostokątnego mają długości 10,24,26. Oblicz długość wysokości opuszczonej na przeciwprostokątną.

Rozwiązanie

Zaczynamy od rysunku

PIC

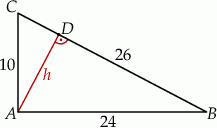
Sposób I

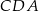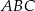Zauważmy, że trójkąty CDA i ABC mają wspólny kąt 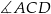∡ACD oraz oba są prostokątne. Zatem muszą to być trójkąty podobne. Zapiszmy proporcje odpowiadających sobie boków i wyznaczmy z niej wysokość

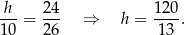
-h- 24- 120- 1 0 = 26 ⇒ h = 13 .

Sposób II

Liczymy pole trójkąta 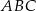ABC z wykorzystaniem dwóch różnych wysokości i porównujemy otrzymane wyniki

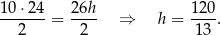
10-⋅24-= 26h- ⇒ h = 120-. 2 2 13

 
Odpowiedź: h = 120- 13

Wersja PDF