Zadanie nr 9644693
Wysokość 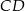 trójkąta
trójkąta 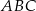 ma długość 12, bok
ma długość 12, bok 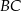 ma długość 37, a odcinek
ma długość 37, a odcinek 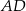 ma długość 5 (zobacz rysunek).
ma długość 5 (zobacz rysunek).
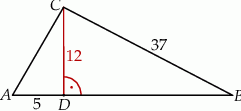
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 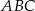 jest prostokątny. jest prostokątny. | P | F |
Miara kąta 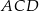 jest równa jest równa 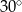 . . | P | F |
Rozwiązanie
Stosujemy twierdzenie Pitagorasa w trójkątach 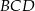 i
i 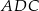 .
.
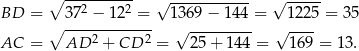
Zauważmy teraz, że
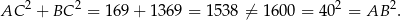
To oznacza, że trójkąt 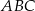 nie jest prostokątny.
nie jest prostokątny.
Gdyby 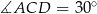 , to trójkąt
, to trójkąt 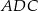 byłby połówką trójkąta równobocznego o boku
byłby połówką trójkąta równobocznego o boku 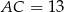 . Ale wtedy
. Ale wtedy 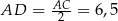 , co oczywiście nie jest prawdą. To oznacza, że
, co oczywiście nie jest prawdą. To oznacza, że 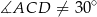 .
.
Odpowiedź: F, F

