Zadanie nr 9841505
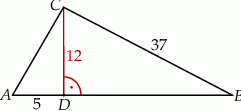
Wysokość 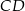 trójkąta
trójkąta 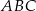 ma długość 12, bok
ma długość 12, bok 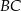 ma długość 37, a odcinek
ma długość 37, a odcinek 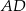 ma długość 5 (zobacz rysunek).
ma długość 5 (zobacz rysunek).
Pole trójkąta 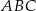 jest równe A/B.
jest równe A/B.
A) 240 B) 210
Obwód trójkąta 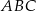 jest równy C/D.
jest równy C/D.
C) 90 D) 120
Rozwiązanie
Stosujemy twierdzenie Pitagorasa w trójkącie 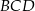 .
.
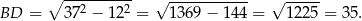
Pole trójkąta  jest więc równe
jest więc równe
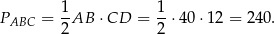
Stosujemy jeszcze twierdzenie Pitagorasa w trójkącie 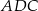 .
.
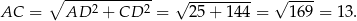
Obwód trójkąta jest więc równy
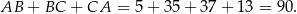
Odpowiedź: A, C

