/Studia/Analiza/Funkcje/Badanie funkcji/Granice

Zadanie nr 3540590

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz granicę 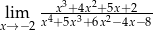--x3+-4x2+-5x+-2-- xli→m−2x4+ 5x3+ 6x2− 4x− 8 .

Rozwiązanie

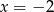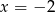Wstawiając x = − 2 do licznika i mianownika łatwo się przekonać, że mamy do czynienia z wyrażeniem postaci 00 . Skoro obydwa wielomiany zerują się w x = − 2 , to muszą się dzielić przez 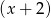(x+ 2) . Wykonajmy to dzielenie (my zrobimy to grupując wyrazy).

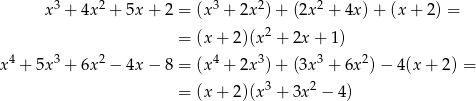
x3 + 4x2 + 5x + 2 = (x 3 + 2x 2)+ (2x 2 + 4x)+ (x+ 2) = 2 = (x + 2)(x + 2x + 1) x 4 + 5x 3 + 6x2 − 4x − 8 = (x 4 + 2x 3)+ (3x 3 + 6x2)− 4(x+ 2) = = (x + 2)(x 3 + 3x 2 − 4)

Zatem

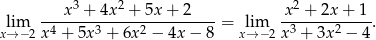
x3 + 4x2 + 5x + 2 x2 + 2x + 1 lim ------------------------= lim ------------. x→ −2 x4 + 5x3 + 6x2 − 4x − 8 x→ −2 x3 + 3x2 − 4

Wstawiamy teraz 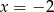x = −2 i otrzymujemy wyrażenie 1 0 . No więc jest to prawie koniec, bo to oznacza, że będziemy mieli 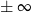± ∞ , ale żeby wiedzieć jaki wybrać znak, musimy ustalić, jaki jest znak mianownika w okolicach 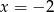x = − 2 . Aby to zrobić, ponownie dzielimy go przez x + 2 .

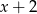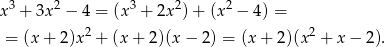
x3 + 3x2 − 4 = (x3 + 2x2) + (x2 − 4) = = (x+ 2)x2 + (x + 2)(x − 2) = (x + 2 )(x2 + x− 2).

Rozkładamy jeszcze trójmian w nawiasie, można z 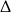Δ -y, ale można też wprost:

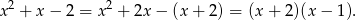
x2 + x− 2 = x2 + 2x − (x + 2) = (x + 2)(x− 1).

W takim razie mamy

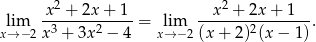
-x2 +-2x+--1- --x-2 +-2x-+-1-- xl→im− 2x3 + 3x2 − 4 = xli→m−2(x + 2 )2(x− 1).

Widać teraz, że mianownik jest ujemny w okolicach 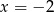x = − 2 , więc

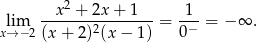
x2 + 2x + 1 1 lim -------2--------= -−- = − ∞ . x→ − 2(x + 2) (x − 1) 0

 
Odpowiedź: − ∞

Wersja PDF