/Konkursy/Zadania testowe/Geometria/Planimetria/Układ współrzędnych/Współrzędne punktów

Zadanie nr 7929402

Dodaj do ulubionych
Dodaj do rozwiązanych

Na płaszczyźnie wprowadzono układ współrzędnych. W początku układu współrzędnych siedzi kangur, który może wykonywać tylko skoki długości 1, przy czym każdy skok jest równoległy do którejś z osi układu. Ile jest punktów płaszczyzny, w których może znaleźć się kangur po wykonaniu dziesięciu skoków?
A) 121 B) 100 C) 400 D) 441 E) Inna liczba

Rozwiązanie

Zauważmy, że po każdym skoku jedna współrzędna punktu, w którym stoi kangur zmieniają się o 1. W takim razie, po parzystej liczbie skoków, końcowy punkt musi mieć parzystą sumę współrzędnych. Ponadto suma wartości bezwzględnych współrzędnych nie może być większa niż 10. Z drugiej strony powinno być jasne, że te warunki są wystarczające – do każdego takiego punktu kangur może dotrzeć w 10 ruchach. Musimy więc policzyć ile jest punktów, których współrzędne spełniają te dwa warunki.

Sposób I

Mamy cztery punkty z jedną z współrzędnych równą 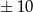± 10 :

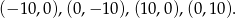
(− 10,0),(0,− 10),(10,0),(0,1 0).

Podobnie jest jeżeli jedna ze współrzędnych jest równa 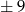± 9 , ale teraz zamiast 0 mamy 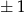± 1 , co daje nam 8 możliwości.

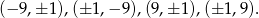
(− 9,± 1),(± 1,− 9),(9,± 1),(± 1,9).

Jeżeli jedna ze współrzędnych jest równa 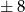± 8 , to druga musi być równa 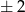± 2 lub 0, więc jest 12 takich punktów (jak poprzednio, ale teraz zamiast 0 możemy wpisać jedną z 3 liczb).
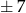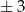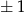Jeżeli jedna ze współrzędnych jest równa ± 7 , to druga musi być równa ± 3 lub ± 1 , więc jest 16 takich punktów.
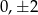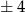Jeżeli jedna z współrzędnych jest równa 6, to druga musi być równa 0 ,± 2 lub ± 4 . Daje to nam 20 możliwości.
Pozostało policzyć punkty, których wartości bezwzględne obu współrzędnych są co najwyżej równe 5. W takiej sytuacji jest trochę łatwiej, bo nie mam już ograniczenia na sumę. Jeżeli obie współrzędne są parzyste, to wybieramy je spośród liczb 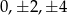0 ,± 2 ,± 4 , więc jest

5 ⋅5 = 25

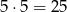
ich takich punktów (każdą współrzędną można wybrać na 5 sposobów).
Jeżeli natomiast obie są nieparzyste, to wybieramy jest spośród liczb 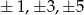± 1,± 3,± 5 , więc jest ich

6 ⋅6 = 36.

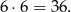
W sumie jest więc

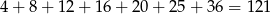
4 + 8 + 12 + 1 6+ 2 0+ 25+ 36 = 121

możliwości.

Sposób II

Tym razem policzmy to trochę inaczej. Par z jedną współrzędną równą 0 jest

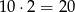
10⋅ 2 = 20

(niezerową liczbę możemy wybrać na 10 sposobów (musi być parzysta) i jeszcze musimy wybrać czy stoi na pierwszym czy na drugim miejscu). Jest też jeden punkt z obiema współrzędnymi 0.

Teraz zajmijmy się tylko punktami o niezerowych współrzędnych. Najpierw policzmy takie, w których współrzędne 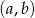(a,b) są dodatnie i 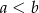a < b . Można wypisać wszystkie:

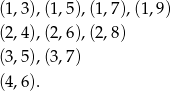
(1,3),(1,5 ),(1 ,7),(1,9) (2,4),(2,6 ),(2 ,8) (3,5),(3,7 ) (4,6).

W każdej z takich par możemy zamienić kolejność liczb oraz przy każdej z liczb możemy zmienić znak na przeciwny. Daje nam to

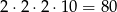
2 ⋅2⋅2 ⋅10 = 80

możliwości.

Pozostały nam jeszcze pary pochodzące od par typu 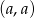(a,a) . Liczbę a możemy wybrać na 5 sposobów (od 1 do 5) i potem możemy zmienić znaki, co daj nam

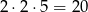
2⋅ 2⋅5 = 20

możliwości.

Razem mamy więc

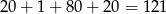
2 0+ 1+ 8 0+ 20 = 121

możliwości.

Zadanie ma prostą interpretację geometryczną. Jeżeli zaznaczymy w układzie współrzędnych skrajne punkty, do których może dojść kangur, to otrzymamy kwadrat, na którego boku jest 11 punktów. Punkty, które liczymy są punktami otrzymanymi na przecięciach linii równoległych do boków tego kwadratu i łączących te wyróżnione punkty na brzegu. W sumie jest ich więc 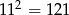11 2 = 121 .

PIC

 
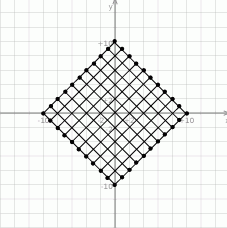
Odpowiedź: A

Wersja PDF