Zadanie nr 1825902
Ile jest liczb 2008–cyfrowych, których każde dwie kolejne cyfry tworzą liczbę podzielną przez 17 lub przez 23?
A) 5 B) 6 C) 7 D) 9 E) Więcej niż 9
Rozwiązanie
Wypiszmy najpierw dwucyfrowe wielokrotności 17 i 23
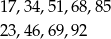
Zauważmy, że każda cyfra z wyjątkiem 6 i 7 jednoznacznie wyznacza kolejną cyfrę, 7 nie wyznacza żadnej cyfry, a 6 wyznacza dwie. Ponadto, jeżeli po 6 wybierzemy 8, to mamy ciąg 6,8,5,1,7 którego nie można już kontynuować – nazwijmy ten ciąg typem I. Jeżeli natomiast po 6 wybierzemy 9, to mamy
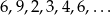
i jesteśmy w punkcie wyjścia, nazwijmy ten ciąg typem II.
Widzimy zatem, że jedynym sposobem pisania długich liczb o podanej własności jest iterowanie ciągu typu II i ewentualnie zmiana na ciąg typu I w końcówce.
Ciagów, które nie zawierają ciągu typu I w końcówce jest tyle ile wyborów pierwszej cyfry dla danej liczby, czyli 5 (mamy do wyboru 6,9,2,3,4).
Jeżeli w końcówce mamy kawałek ciągu typu I, to na tę końcówkę mamy 4 możliwości
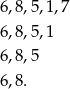
Cała reszta danej liczby jest już jednoznacznie wyznaczona (bo jest typu II).
Jest zatem 9 takich liczb.
Odpowiedź: D

