Zadanie nr 5720751
Liczba 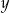 jest sumą cyfr liczby naturalnej
jest sumą cyfr liczby naturalnej  , a liczba
, a liczba  jest sumą cyfr liczby
jest sumą cyfr liczby 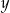 . Dla ilu liczb naturalnych
. Dla ilu liczb naturalnych  zachodzi równość
zachodzi równość 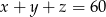 ?
?
A) 0 B) 1 C) 2 D) 3 E) Więcej niż 3
Rozwiązanie
Oczywiście liczba  musi być dwucyfrowa i mniejsza niż 60. W takim razie jej suma cyfr
musi być dwucyfrowa i mniejsza niż 60. W takim razie jej suma cyfr 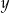 nie będzie większa niż 9+5=14. Wtedy
nie będzie większa niż 9+5=14. Wtedy 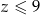 . Mamy zatem
. Mamy zatem 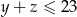 , co daje
, co daje 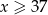 . Oznaczmy
. Oznaczmy 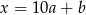 , gdzie
, gdzie 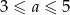 . Wtedy
. Wtedy 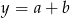 oraz
oraz 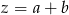 (jeżeli
(jeżeli 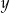 jest jednocyfrowa) lub
jest jednocyfrowa) lub 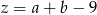 (jeżeli
(jeżeli 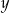 jest dwucyfrowa). W pierwszym przypadku
jest dwucyfrowa). W pierwszym przypadku
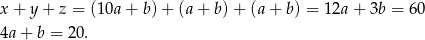
Wszystkie rozwiązania tego równania to 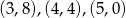 . Pierwsze odrzucamy bo daje
. Pierwsze odrzucamy bo daje 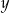 dwucyfrowe, a dwa następne dają nam liczby 44 i 50.
dwucyfrowe, a dwa następne dają nam liczby 44 i 50.
W drugim przypadku
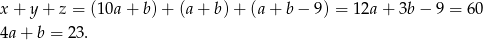
Rozwiązania tego równania to 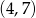 i
i 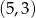 . Drugie odrzucamy, bo prowadzi do jednocyfowego
. Drugie odrzucamy, bo prowadzi do jednocyfowego 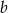 a z pierwszego dostajemy liczbę 47.
a z pierwszego dostajemy liczbę 47.
Odpowiedź: D

