Zadanie nr 9809758
Ile liczb trzycyfrowych podzielnych przez 9 ma następującą własność: suma cyfr ilorazu tej liczby przez 9 jest o 9 mniejsza od sumy jej cyfr?
A) 1 B) 2 C) 4 D) 5 E) 11
Rozwiązanie
Niech  będzie liczbą spełniającą warunek z treści zadania. Ponieważ
będzie liczbą spełniającą warunek z treści zadania. Ponieważ  jest podzielna przez 9, to przez dziewięć dzieli się też suma jej cyfr. Jest ona zatem równa 9,18 lub 27. 9 i 27 łatwo wyeliminować, gdyż suma cyfr liczby
jest podzielna przez 9, to przez dziewięć dzieli się też suma jej cyfr. Jest ona zatem równa 9,18 lub 27. 9 i 27 łatwo wyeliminować, gdyż suma cyfr liczby  równa 9 oznacza, że
równa 9 oznacza, że 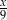 ma sumę cyfr równą 0, co jest niemożliwe. Podobnie, gdy suma cyfr jest równa
ma sumę cyfr równą 0, co jest niemożliwe. Podobnie, gdy suma cyfr jest równa 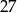 , to
, to 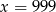 i
i 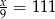 i się nie zgadza.
i się nie zgadza.
Zatem suma cyfr liczby  wynosi 18, a więc suma cyfr liczby
wynosi 18, a więc suma cyfr liczby 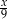 wynosi
wynosi 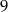 . W szczególności,
. W szczególności, 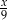 dzieli się przez 9, czyli
dzieli się przez 9, czyli  dzieli się przez 81. Teraz wystarczy posprawdzać wszystkie wielokrotności 81 mniejsze od 1000. Jak się to zrobi, to okazuje się, że liczb o opisanej własności jest 5: 486,567,648,729,972.
dzieli się przez 81. Teraz wystarczy posprawdzać wszystkie wielokrotności 81 mniejsze od 1000. Jak się to zrobi, to okazuje się, że liczb o opisanej własności jest 5: 486,567,648,729,972.
Odpowiedź: D

