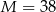Zadanie nr 2870517
Wyznacz najmniejszą 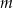 i największą
i największą 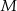 wartość funkcji
wartość funkcji 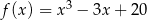 w przedziale
w przedziale 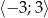 .
.
Rozwiązanie
Aby zobaczyć jak zmienia się funkcja 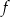 (gdzie rośnie, maleje itd.), liczymy pochodną
(gdzie rośnie, maleje itd.), liczymy pochodną
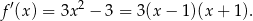
Widzimy zatem, że pochodna jest dodatnia (a więc wyjściowa funkcja rośnie) na przedziałach 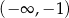 i
i 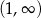 oraz pochodna jest ujemna (wyjściowa funkcja maleje) na przedziale
oraz pochodna jest ujemna (wyjściowa funkcja maleje) na przedziale 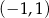 . Najlepiej sobie to naszkicować – my od razu narysujemy dokładny wykres, ale tak naprawdę w zupełności wystarczy szkic, jak funkcja rośnie i maleje.
. Najlepiej sobie to naszkicować – my od razu narysujemy dokładny wykres, ale tak naprawdę w zupełności wystarczy szkic, jak funkcja rośnie i maleje.
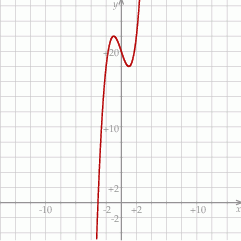
Ponieważ funkcja ma minimum lokalne w punkcie 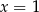 i na prawo od tego punktu rośnie, to najmniejsza wartość na przdziale
i na prawo od tego punktu rośnie, to najmniejsza wartość na przdziale 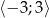 to
to 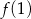 lub
lub 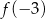 . Liczymy, która z tych liczb jest mniejsza
. Liczymy, która z tych liczb jest mniejsza
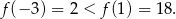
Zatem 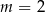 . Podobnie, największa wartośc to
. Podobnie, największa wartośc to 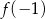 lub
lub 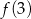 . Liczymy
. Liczymy
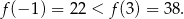
Zatem 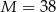 .
.
Odpowiedź: 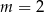 ,
,