/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne

Zadanie nr 3504610

Dodaj do ulubionych
Dodaj do rozwiązanych

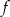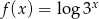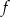Funkcja f jest określona wzorem x f(x ) = lo g3 dla każdej liczby rzeczywistej x . Oblicz pochodną funkcji f w punkcie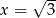 √ -- x = 3

Rozwiązanie

Zauważmy, że korzystając ze wzoru na zmianę podstawy logarytmu możemy wzór danej funkcji zapisać w postaci

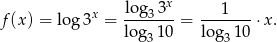
x f(x ) = lo g3x = log3-3- = ---1--- ⋅x. log31 0 log 310

Pochodna tej funkcji jest więc równa

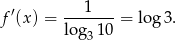
f′(x) = ---1--- = lo g3. log 310

 
Odpowiedź: f ′(√ 3) = --1---= log 3 log310

Wersja PDF