/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne

Zadanie nr 4067251

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz ekstrema funkcji 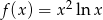2 f (x) = x ln x .

Rozwiązanie

Ze względu na logarytm dziedziną funkcji 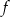f jest przedział (0,+ ∞ ) .

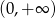Liczymy pochodną

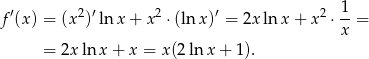
f′(x) = (x2)′ln x+ x2 ⋅(ln x)′ = 2x ln x + x2 ⋅ 1-= x = 2x lnx + x = x(2ln x + 1).

Ponieważ 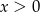x > 0 wystarczy badać znak wyrażenia w nawiasie. Sprawdźmy kiedy jest dodatnie.

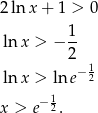
2 ln x + 1 > 0 ln x > − 1- 2 ln x > ln e−12 x > e−12.

Widać teraz, że w punkcie 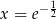x = e− 12 pochodna zmienia znak z ujemnego na dodatni, czyli funkcja 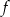f ma w tym punkcie minimum lokalne.

Policzmy jeszcze wartość funkcji w tym punkcie

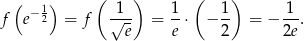
( ) ( ) ( ) f e− 12 = f √1- = 1⋅ − 1- = − 1-. e e 2 2e

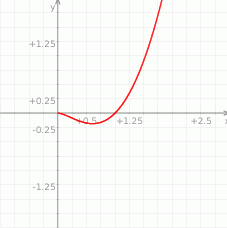
Na koniec obrazek.

PIC

 
Odpowiedź: Minimum w 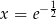1 x = e− 2 , − 12 -1 f (e ) = − 2e

Wersja PDF