Zadanie nr 5565500
Udowodnij nierówność Bernoulliego: jeżeli 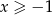 i
i 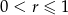 , to
, to 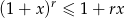 .
.
Rozwiązanie
Podstawmy w nierówności, którą mamy udowodnić 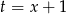 . Musimy zatem udowodnić nierówność
. Musimy zatem udowodnić nierówność
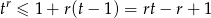
przy założeniu: 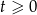 i
i 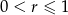 . Jeżeli
. Jeżeli 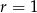 , to nierówność jest oczywiście spełniona, więc załóżmy dalej, że
, to nierówność jest oczywiście spełniona, więc załóżmy dalej, że 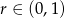 .
.
Badamy funkcję 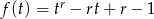 . Liczymy jej pochodną.
. Liczymy jej pochodną.
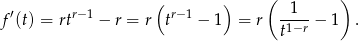
Zauważmy teraz, że (przy naszych założeniach o  i
i 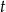 )
) 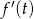 zmienia znak w
zmienia znak w 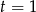 z dodatniego na ujemny, więc
z dodatniego na ujemny, więc 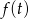 ma w
ma w 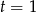 maksimum. Stąd
maksimum. Stąd
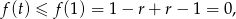
a to jest dokładnie nierówność, którą mieliśmy udowodnić.

