Zadanie nr 1876811
Każda z liczb 257,338 ma tę własność, że jeśli jej cyfry zapiszemy w odwrotnej kolejności, to otrzymamy liczbę od niej większą. Ile jest wszystkich liczb trzycyfrowych o tej własności?
A) 124 B) 252 C) 280 D) 288 E) 360
Rozwiązanie
Własność o której mowa w treści zadania to dokładnie pytanie kiedy cyfra jedności jest większa niż cyfra setek. Zamiast liczyć te liczby łatwiej policzyć jest wszystkie liczby trzycyfrowe, które mają cyfrę setek inną niż cyfrę jedności, i których cyfra jedności nie jest 0. Szukane liczby to dokładnie połowa tego zbioru.
Wszystkich liczb 3 cyfrowych jest 900. Liczb z identyczną cyfrą setek i jedności jest 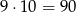 (9 odpowiada cyfrze setek, a 10 cyfrze dziesiątek). Musimy jeszcze odjąć liczby z 0 na końcu, jest ich 90. Zatem liczb trzycyfrowych z nieidentycznymi cyframi setek i jedności, i niezerową cyfrą jedności jest 720. Dokładnie połowa z nich ma żądaną własność.
(9 odpowiada cyfrze setek, a 10 cyfrze dziesiątek). Musimy jeszcze odjąć liczby z 0 na końcu, jest ich 90. Zatem liczb trzycyfrowych z nieidentycznymi cyframi setek i jedności, i niezerową cyfrą jedności jest 720. Dokładnie połowa z nich ma żądaną własność.
Odpowiedź: E

