Zadanie nr 8096004
Jeżeli każdy z wierzchołków 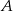 i
i 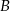 trójkąta
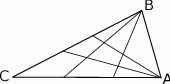
trójkąta 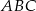 połączymy odcinkami z dwoma różnymi punktami leżącymi na przeciwległym boku, to odcinki te podzielą ten trójkąt na dziewięć części (patrz rysunek). Na ile części zostanie podzielony trójkąt, jeżeli każdy z wierzchołków
połączymy odcinkami z dwoma różnymi punktami leżącymi na przeciwległym boku, to odcinki te podzielą ten trójkąt na dziewięć części (patrz rysunek). Na ile części zostanie podzielony trójkąt, jeżeli każdy z wierzchołków 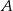 i
i 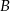 połączymy odcinkami z czterema punktami (różnymi od wierzchołków) leżącymi na przeciwległym do nich boku?
połączymy odcinkami z czterema punktami (różnymi od wierzchołków) leżącymi na przeciwległym do nich boku?
A) 16 B) 25 C) 36 D) 42 E) 49
Rozwiązanie
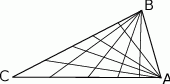
Każda kolejna prosta pozioma utworzy trzy nowe części, czyli po dorysowaniu dwóch będzie 15 części. Jeżeli teraz dorysujemy prostą pionową, to będziemy mieli 5 nowych części. Dorysowujemy dwie, czyli dostajemy 10 nowych części. W sumie mamy 25 części.
Można też oczywiście zrobić rysunek i te części po prostu policzyć.
Odpowiedź: B

