/Konkursy/Zadania testowe/Kombinatoryka/Liczenie ilości liczb o własności...

Zadanie nr 7539712

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest kula o promieniu 3 i o środku w początku układu współrzędnych. Ile punktów na powierzchni tej kuli ma wszystkie współrzędne całkowite?
A) 30 B) 24 C) 12 D) 6 E) 3

Rozwiązanie

Równanie takiej kuli jest postaci

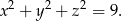
2 2 2 x + y + z = 9.

Musimy ustalić ile jest rozwiązań całkowitych tego równania.

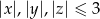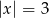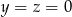Oczywiście |x|,|y|,|z| ≤ 3 . Ponadto jeżeli np. |x| = 3 , to y = z = 0 . Mamy zatem 6 rozwiązań

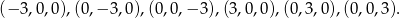
(−3 ,0,0),(0,− 3,0),(0,0,− 3),(3,0,0),(0,3,0 ),(0 ,0,3).

Przynajmniej jedna z liczb musi być równa 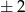± 2 (bo inaczej suma będzie mniejsza od 9), powiedzmy, że 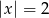|x| = 2 . Wtedy mamy równanie

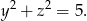
2 2 y + z = 5.

Jedyne rozwiązania tego równania to 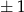± 1 i ± 2 .

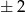Pozostało policzyć ile jest możliwych układów 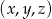(x ,y ,z) o tej własności, że liczby te są równe (w pewnej kolejności) 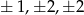± 1 ,± 2 ,± 2 . Mamy 3 możliwości ustalenia gdzie będzie 1, oraz 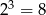3 2 = 8 mozliwości dopisania znaków do tych liczb. W sumie mamy zatem 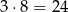3⋅8 = 24 możliwości. W połączeniu z 6 rozwiązaniami znalezionymi wcześniej mamy 30 rozwiązań.  
Odpowiedź: A

Wersja PDF